Introduction
既存の手法にノイズ遷移行列、reweighting、label correction、サンプル選択などがあるが、いずれもモデルが十分に訓練されてない段階での予測結果に強く依存するし、各サンプルを独立的に扱って大域的な構造については捉えてない。よって、局所最適解にいきがち。
既存の手法はこちら: 📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future
最適輸送によるPseudo LabelをUnlabeledへの付与は、サンプルとクラスの間の距離ととらえれば使える。しかし、問題として決定境界が十分に正確ではない場合、距離が近い2つのサンプルが、論理的に遠いクラスの中心に割り当てられる可能性があるらしい。
最適輸送はつまり大域的に見れてないということ。
この論文では最適輸送によるPseudo labelの付与に、大域的な構造を加味させる手法を提案した。局所的な一貫性と大域的な分類可能性を考えたらしい。また、学習ではカリキュラム学習を使うことで、学習の序盤から誤ったPseudo Labelによる影響を減らした。
カリキュラム学習の詳細はこちら: 📄2018-ICML-MentorNet: Learning Data-Driven Curriculum for Very Deep Neural Networks on Corrupted Labels
この論文の貢献は以下のとおりである。
- 局所的一貫性、大域的な分類可能性?を考慮した、最適輸送によるPseudo Label付与の学習手法を提案した。
- CSOTという最適輸送にCurriculumを盛りこんだ改良版最適輸送を作った。
- CSOTを計算するための高速化アルゴリズムを開発した。
- 既存の手法と比べてみていい結果出たと改めて分かった。
Related Work
自分のための読むべきリストみたいなものでもある。
PUについてのOptimal Transportの初出。
📄2020-NIPS-Partial Optimal Transport with Applications on Positive-Unlabeled Learning
Noisy Label
- 📄
2019-CVPR-[PENCIL]Probabilistic End-To-End Noise Correction for Learning With Noisy Labels
- 📄
2019-PMLR-[SELFIE] Refurbishing Unclean Samples for Robust Deep Learning
Curriculum Learning
問題設定
最適輸送
ベクトルが存在するとき、遷移コスト行列をまず定義する。最適輸送とは、を定義し、以下の式を最小化する。ちなみにこれは、Frobenius Dot Productという名前らしい。
とはPolytope=多面体であり、以下のように数式的に書いてあるが、各行ともに和がの各成分と一致し、各列ともに和がの各成分と一致するということ。
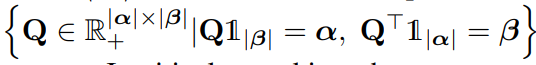
つまりやってることはからへ輸送したい。からへ輸送するコストがであり、輸送する量がである。は各行ごとに和がに一致し、各列ごとにに一致しないといけない。
最適輸送によるPseudo Label
バッチサイズがで、クラス分類をする時を考える。
運ぶ元のVectorはで、運ぶ先はである。Softmax分類器分類した結果をとする。ここで、コスト行列をとする。これによって、0に近いsoftmaxは高いコストに、1に近いsoftmaxは低いコストになる。そして、以下のような最適輸送を計算する。
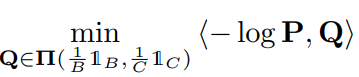
の制約として、各行の総和はそれぞれ、各列の総和がである。
これを計算することで、各クラスとしては所属するデータの総量が決まっている中で、どのサンプルから運んでくるのが一番コスト安いのか?の兼ね合いを求められる。その兼ね合いによってDenoisingしている感じ。
と乗じて正規化することによって、はバッチの番目のサンプルが、クラスへ運搬する=所属する重み。つまり、最適輸送の計算結果を所属だとみなせば、局所性をある程度考慮したNoisy Labelに対してのロバスト性になる。
伝統的な最適輸送においてのSinkhorn Algorithm
直接最適輸送を計算するのは難しい。ここで、エントロピー正則化項を加えて以下の式を正則化する。
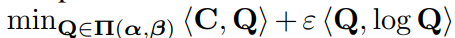
この形にするとSinkhorn Algorithmによって計算しやすく、GPUを利用した計算もできるようになる。
Methodology
クラス分類の訓練データセットを使って訓練する。しかし、Noisy Labelであるという前提である。
局所構造込みの最適輸送によるノイズ除去と再ラベル(SOT)
既存の最適輸送ベースの手法は大域的な最適化をするが、局所的な最適化は行わない。ここでは、局所的な構造(近くのラベルは何?)を考慮した最適輸送を開発した。
前述のように、をバッチで番目のサンプルがクラスに属する確率だとして、最適輸送のコストをとして扱う手法である。この手法ではそれにとどまらず、ハイパラに制御された2つの正則化項で局所的な構造を捉えられるようにした。
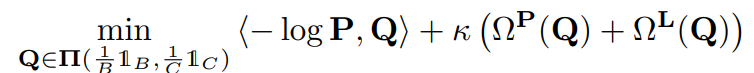
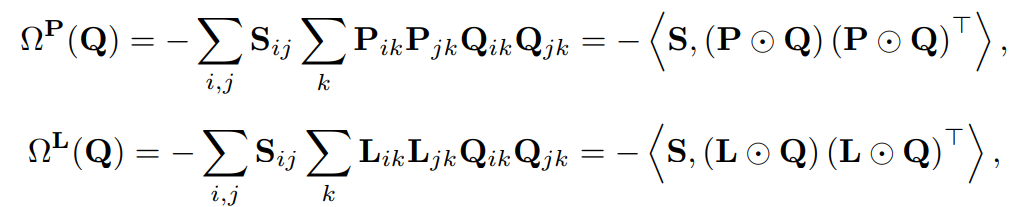
- であり、はバッチの番目のサンプルのcosine類似度
- であり、はone-hotベクトルであり、与えられたラベルを表す(Noisyなものであるが)
- であり、はバッチの番目のサンプルが各クラスに所属する確率を表す。
- とすることで所属する確率が高いクラスはコスト低く、確率が低いクラスのコストは爆発的に大きくしている。
は、のサンプル間で、以下の条件を満たせば満たすほど、2つのサンプルのそれぞれクラスへ輸送する量の積に大きい重みにしている。
- cosine類似度が高い。
- つまり入力空間の上で近いところにありそう。
- Noisy Labelで訓練したときのクラスについてのサンプルの予測確率が同様に高い。
- つまり、Noisy Labelで訓練した識別器でも同じクラスに属していると判断されてる。
つまり、cosine類似度が高いという条件を付けたことによって、入力が近くないと損失関数を大きく減らすことができないようにした。
同様に、は、同様にサンプルのクラスへの輸送について以下の条件を満たすほど大きくした。
- cosine類似度が高い。
- 与えられたNoisy Labelについて、同じくクラスに属していれば1、それ以外ならば0。
- 隣接したものについてを考えることができるらしい。十分に識別器がNoisy Labelに近似できない前提だからこの項を追加した??これいらなくね。
このように訓練することが、周辺構造を考慮した最適輸送となる。
Curriculumと周辺構造を考慮した最適輸送(CSOT)
訓練の早期段階や、Noise率が非常に高い場合、予測結果は十分に信頼できない。これに対して、カリキュラム学習の要領で解決を試みた。
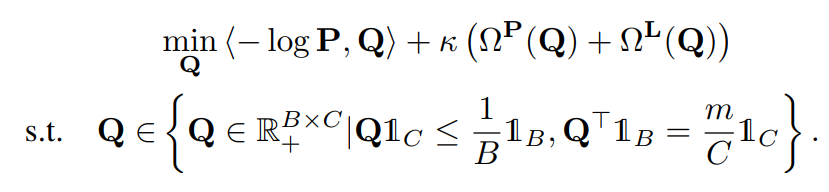
無印SOTと異なるところは、の予算という値を導入した。そして、各行の和はのままだが、各列の和はではなく、予算を用いたより小さくできるである。(最終的にするので各行の和は1になる。)
学習の早い段階orNoise率が高いとき、などとすることによって、全体の50%だけ輸送させることになる。この時、輸送されるのは上位50%の信頼できるラベル付け=コストが最も低い50%の輸送=運びやすい輸送=上位50%の間違ってなさそうなサンプルを運ばせることができる。これでカリキュラム学習を実現させている。
最後に、DataをCleanとCorruptedの2つの集合に分ける。
最適輸送によって計算咲いた後のラベル付け自体はである。
を考える。これは各ラベルの自信度合いであるといえる。そして、毎イテレーションごとに、重みが大きい=自信があるラベル付けのサンプルから順に個選ぶ。の割合だけ輸送したので、信頼できると思えるものもの割合だけ選ぶ。
そして信頼できるもの、できないものの2つの集合に切り分けるできる。
切り分けた後の学習
Noisy Labelあるあるの早期での間違ったラベル付け換えによる影響を避けるため、2段階の訓練スキームを考えた。
- 第1段階では、徐々に選択されたCleanなサンプルで教師あり学習をして、選ばれなかったラベルで自己教師あり学習をする。
- 第2段階では、すべてのCleanなサンプルで自己教師あり学習をする。
損失関数は、教師ありと自己教師ありはそれぞれ以下のように設計する。先行研究のNCEとSimSiamで提案されたものを使う。はMix-up損失。はNCEで提案された。はSimSiamで提案された。
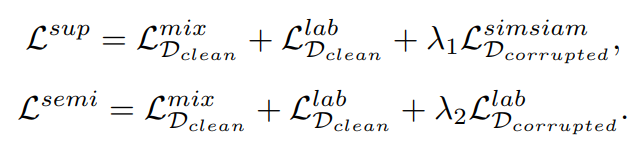
CSOTを計算するための軽量なソルバの提案
局所一貫性を考慮しないCOTの計算
まずは、局所一貫性を考慮しない、カリキュラム学習だけをとりこんだ最適輸送の計算を考える。
既存のやり方と同様に、エントロピーの項をつける。
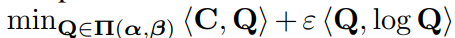
そして、これは先行研究(Jean-David Benamou, Guillaume Carlier, Marco Cuturi, Luca Nenna, and Gabriel Peyré. Iterative bregman projections for regularized transportation problems. SIAM Journal on Scientific Computing, 37(2):A1111–A1138, 2015.)によって、KLダイバージェンスでの最適化で近似できる。
これは、Dykstra’s algorithm https://www.jstor.org/stable/2288193によって解くことができる。
局所一貫性を考慮したCSOTの計算
では考慮するときはどのように説くことができるか。Generalized Conditional Gradient(GCG)というアルゴリズムの枠内を使って解く。


Experiment
からはじめて、80イテレーションの間に1増えるようにした。の上限自体は1で超える分も1にしている。
CSOTは合成ノイズが付与されたCIFAR-10, CIFAR-100で有効だとわかった。対称ノイズ、非対称ノイズのいずれでもいい結果を出した。
実世界のデータセットWebVisionでもいい性能を出した。訓練するためのコストも低い。
Abrasion Study
- Curriculumを導入したことでAccuracyは2%向上した。ノイズが高いときは4%もの改善が見られた。
- CSOTによるCleanとCorruptedへの切り分けの性能も優れている。
- CSOTによる破損したラベル(PUにも応用できね?)修正もよい性能を誇る。
- 効率的なスケーリング反復=Algorithm1を盛り込んだら、最高で3.7倍も速くなった。
